\( \def\RR{\bf R} \def\real{\mathbb{R}} \def\bold#1{\bf #1} \def\d{\mbox{Cord}} \def\hd{\widehat \mbox{Cord}} \DeclareMathOperator{\cov}{cov} \DeclareMathOperator{\var}{var} \DeclareMathOperator{\cor}{cor} \newcommand{\ac}[1]{\left\{#1\right\}} \DeclareMathOperator{\Ex}{\mathbb{E}} \DeclareMathOperator{\diag}{diag} \)

Network Communities and Variable Clustering via CORD


Xi (Rossi) Luo


Brown University
Department of Biostatistics
Center for Statistical Sciences
Computation in Brain and Mind
Brown Institute for Brain Science
The ABCD Research Group


Statistical Learning and Data Science
June 7, 2016


Funding: NSF/DMS (BD2K) 1557467; NIH P20GM103645, P01AA019072, P30AI042853; AHA

Collaborators

Florentina Bunea

Florentina Bunea
Cornell University

Florentina Bunea

Christophe Giraud
Paris Sud University

Data Science Problem

  • We are interested in big cov with many variables
    • Global property for certain joint distributions
    • Real-world cov: maybe non-sparse and other structures
  • Clustering successful for > 40 years and for DSDonoho, 2015
    • Exploratory Data Analysis (EDA)Tukey, 1977
    • Hierarchical clustering and KmeansHartigan & Wong, 1979
    • Usually based on marginal/pairwise distances
  • Can clustering and big cov estimation be combined?

Example: SP 100 Data

  • Daily returns from stocks in SP 100
    • Stocks listed in Standard & Poor 100 Indexas of March 21, 2014
    • between January 1, 2006 to December 31, 2008
  • Each stock is a variable
  • Cov/Cor matrices (Pearson's or Kendall's tau)
    • Re-order stocks by clusters
    • Compare cov patterns with different clustering/ordering

Cor after Grouping by Clusters

Kmeans
Our $G$-models

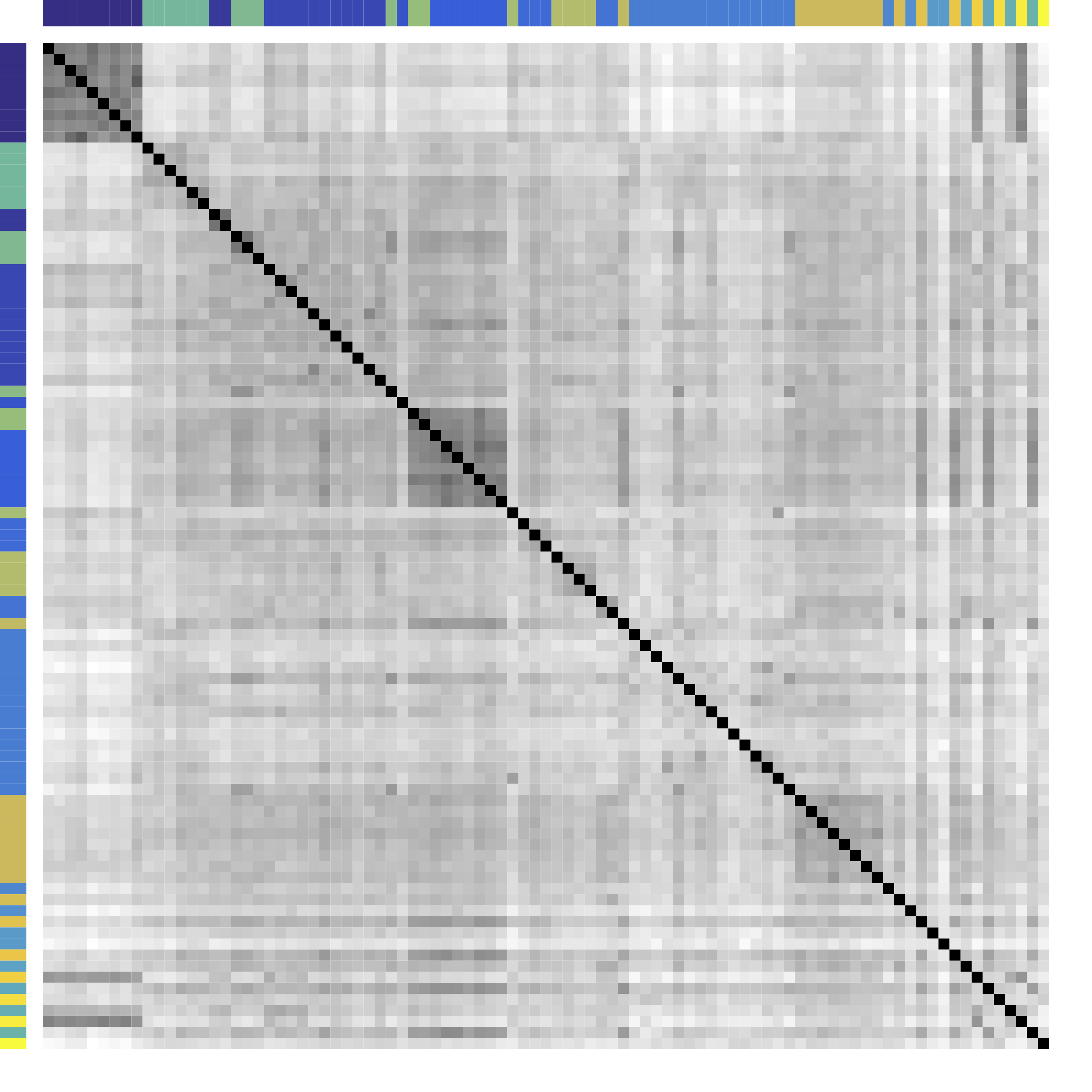
Ours yields stronger off-diagonal, tile patterns. Black = 1.
Color bars: variable groups/clusters
Off-diagonal: correlations across clusters

Clustering Results

Industry Ours Kmeans Hierarchical Clustering
Telecom ATT, Verizon ATT, Verizon, Pfizer, Merck, Lilly, Bristol-Myers ATT, Verizon
Railroads Norfolk Southern, Union Pacific Norfolk Southern, Union Pacific Norfolk Southern, Union Pacific, Du Pont, Dow, Monsanto
Home Improvement Home Depot, Lowe’s Home Depot, Lowe’s, Starbucks Home Depot, Lowe’s, Starbucks, Costco, Target, Wal-Mart, FedEx, United Parcel Service
$\cdots$
All methods yield 30 clusters.

Model

Problem

  • Let ${X} \in \real^p$ be a zero mean random vector
  • Divide variables into partitions/clusters
    • Example: $\{ \{X_1, X_3, X_7\}, \{X_2, X_5\}, \dotsc \}$
  • Theoretical: Find a partition $G = \{G_k\}_{ 1 \leq k \leq K}$ of $\{1, \ldots, p\}$ such that all $X_a$ with $a \in G_k$ are "similar"
  • DS: find a "helpful" partition that show patterns

Related Methods

  • Clustering: Kmeans and hierarchical clustering
    • Advantages: fast, general, popular
    • Limitations: low signal-noise-ratio, theory
  • Community detection: huge literature see review Newman, 2003 but start with observed adjacency matrices

Kmeans



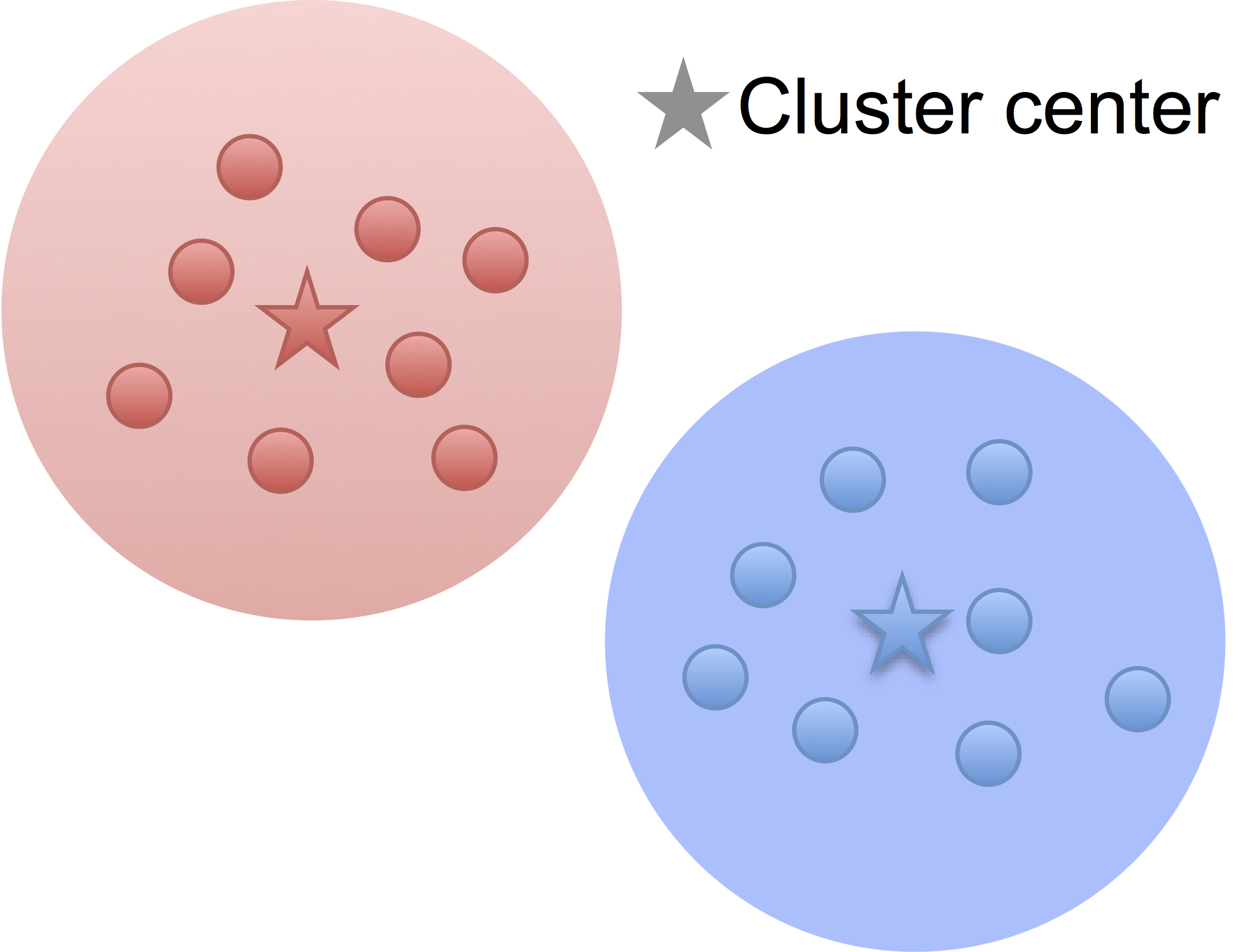
Low noise

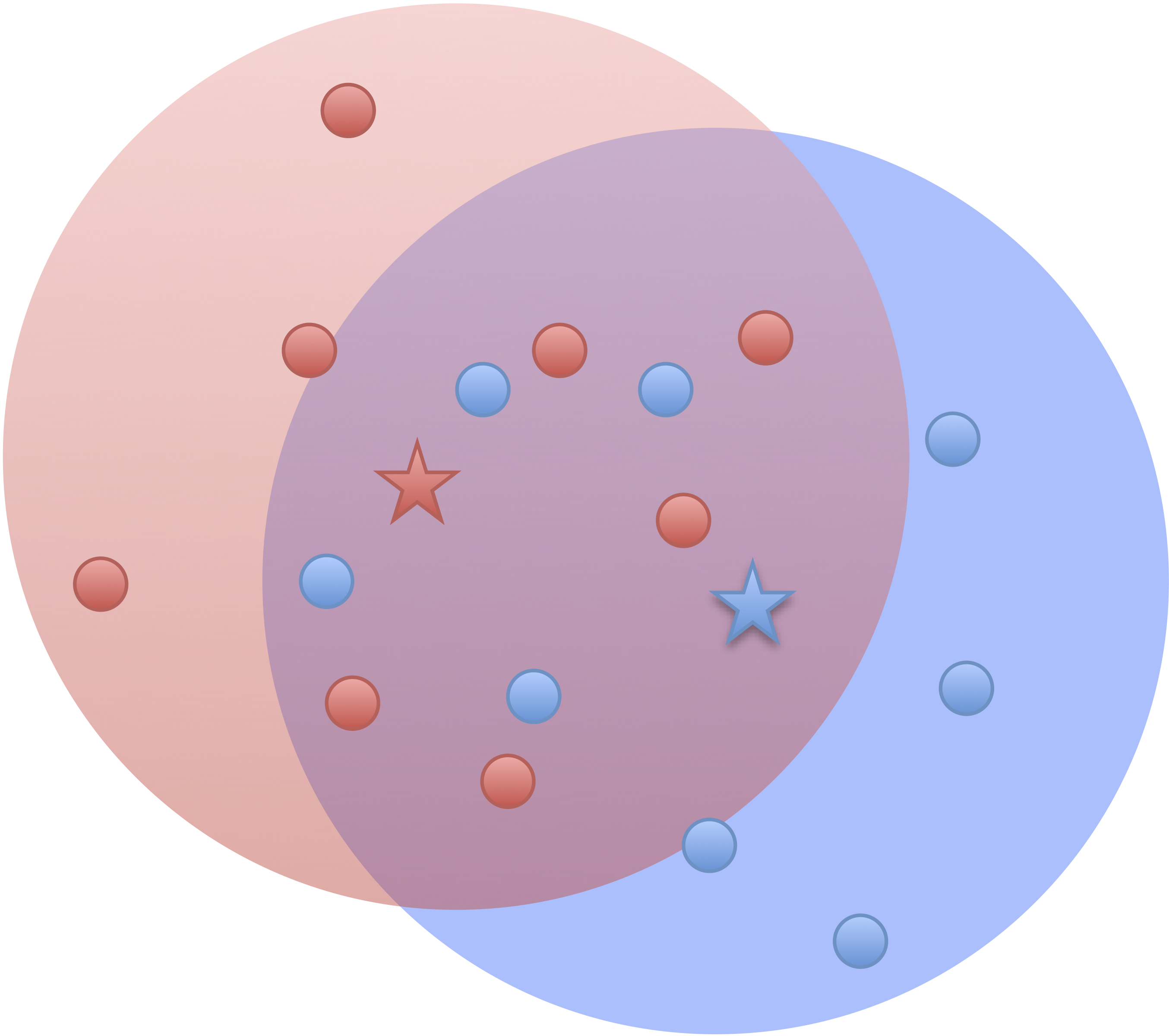
High noise

  • Cluster points together if pairwise distance small
  • Clustering accuracy depends on the noise

Kmeans: Generative Model

  • Data $X_{n\times p}$: $p$ variables from partition $G$: $$G=\{ \{X_1, X_3, X_7\}, \{X_2, X_5\}, \dotsc \}$$
  • Mixture Gaussian: if variable $X_j \in \real^n$ comes from cluster $G_k$ Hartigan, 1975 $$X_{j} = Z_k + \epsilon_j, \quad Z_k \bot \epsilon_j $$
  • Kmeans minimizes over $G$ (and centroid $Z$): $$\sum_{k=1}^K \sum_{j\in G_k} \left\| X_j - Z_k \right\|_2^2 $$
Strictly, Kmeans considers data points in $\real^p$ from $K$ populations

$G$-Latent Cov

  • We call $G$-latent model: $$X_{j} = Z_k + \epsilon_j, \quad Z_k \bot \epsilon_j \mbox{ and } j\in G_k $$
  • WLOG, all variables are standardized
  • Intuition: variables $j\in G_k$ form net communitiesLuo, 2014

Model


$$ X_{n\times p}=\underbrace{Z_{n\times k}}_\text{Source/Factor} \quad \underbrace{G_{k\times p}}_\text{Mixing/Loading} + \underbrace{E_{n\times p}}_{Error} \qquad Z \bot E$$

  • Clustering: $G$ is $0/1$ matrix for $k$ clusters/ROIs
  • Decomposition:
    • PCA/factor analysis: orthogonality
    • ICA: orthogonality → independence
    • matrix decomposition: e.g. non-negativity
  • Observing $X$, we show identifiability for non-diag or even "negative" $\cov(Z)$
  • Can generalize to semiparametric distributions

Principals in Other Clustering

  • The Euclidean distance for hierarchical clustering and Kmeans, for two columns/voxles $X_a$ and $X_b$: $$ \|X_a - X_b \|_2^2 = 2(1-\cor(X_a, X_b)) $$
  • Recall $X_i = Z_k + E_i$ $i \in G_k$; cor depends on $\var(E)$
  • Even worse, if $\var(E)$ or SNRs vary across clusters, the distance between $X_a$ and $X_b$ is
    • larger even if generated by same $Z$ and large error
    • smaller even if generated by different $Z$ and small error

Generalization

Example: $G$-Block

  • Set $G=\ac{\ac{1,2};\ac{3,4,5}}$, $X \in \real^p$ has $G$-block cov
    $$\Sigma =\left(\begin{array}{ccccc} {\color{red} D_1} & {\color{red} C_{11} }&C_{12} & C_{12}& C_{12}\\ {\color{red} C_{11} }&{\color{red} D_1 }& C_{12} & C_{12}& C_{12} \\ C_{12} & C_{12} &{\color{green} D_{2}} & {\color{green} C_{22}}& {\color{green} C_{22}}\\ C_{12} & C_{12} &{\color{green} C_{22}} &{\color{green} D_2}&{\color{green} C_{22}}\\ C_{12} & C_{12} &{\color{green} C_{22}} &{\color{green} C_{22}}&{\color{green} D_2} \end{array}\right) $$
  • Matrix math: $\Sigma = G^TCG + d$
  • We allow $|C_{11} | \lt | C_{12} |$ or $C \prec 0$
    • Kmeans/HC leads to block-diagonal cor matrices (permutation)
  • Clustering based on $G$-Block, generalizing $G$-Latent which requires $C\succ 0$

Defining Order of Partitions

  • $G\leq G^{\prime}$ if $G^{\prime}$ is a sub-partition of $G$
    • Example: $G^{\prime} =\{\{1\}, \{2\}, \{3\}\}$, $G=\{1,2,3\}$
  • Denote $a\stackrel{G(X)}{\sim} b$ by the partition $G(X)$ if $\var(X_{a})=\var(X_{b})$ and $\cov(X_{a},X_{c})=\cov(X_{b},X_{c})$ for all $c\neq a,b$
  • Note that $a\stackrel{G^{\prime}(X)}{\sim} b$ if $G\leq G^{\prime}$
  • Exist multiple partitions that yield $G$-block cov

Minimum $G$ Partition

Theorem: $G^{\beta}(X)$ is the minimal partition induced by $a\stackrel{G^{\beta}}{\sim} b$
iff $\var(X_{a})=\var(X_{b})$ and $\cov(X_{a},X_{c})=\cov(X_{b},X_{c})$ for all $c\neq a,b$. Moreover, if the matrix of covariances $C$ corresponding to the partition $G(X)$ is positive-semidefinite, then this is the unique minimal partition according to which ${X}$ admits a latent decomposition.

The minimal partition is unique under regularity conditions.

Method

New Metric: CORD

  • First, pairwise correlation distance (like Kmeans)
    • Gaussian copula: $$Y:=(h_1(X_1),\dotsc,h_p(X_p)) \sim N(0,R)$$
    • Let $R$ be the correlation matrix
    • Gaussian: Pearson's
    • Gaussian copula: Kendall's tau transformed, $R_{ab} = \sin (\frac{\pi}{2}\tau_{ab})$
  • Second, maximum difference of correlation distances $$\d(a,b) := \max_{c\neq a,b}|R_{ac}-R_{bc}|$$
  • Third, group variables $a$, $b$ together if $\d(a,b) = 0$
  • "The enemy of my enemy is my friend"

Algorithm: Main Idea

  • Greedy: one cluster at a time, avoiding NP-hard
  • Cluster variables together if CORD metric $$\widehat \d(a,b) \lt \alpha$$ where $\alpha$ is a tuning parameter
  • $\alpha$ is chosen by theory or CV

Theory

Condition

Let $\eta \geq 0$ be given. Let ${ X}$ be a zero mean random vector with a Gaussian copula distribution with parameter $R$. $$ \begin{multline} \mathcal{R}(\eta) := \{R: \ \d(a,b) := \max_{c\neq a,b}|R_{ac}-R_{bc}|>\eta\quad \\ \textrm{for all}\ a\stackrel{G(X)}{\nsim}b.\} \end{multline} $$ Group separation condition: $R \in \mathcal{R}(\eta)$.

The signal strength $\eta$ is large.

Consistency

Theorem: Define $\tau=|\widehat R-R|_{\infty}$ and we consider two parameters $(\alpha,\eta)$ fulfilling $$\begin{equation} \alpha\geq 2\tau\quad\textrm{and}\quad \eta\geq2\tau+\alpha. \end{equation}$$ Then, applying our algorithm we have $\widehat G=G(X)$ whp.

Ours recovers the exact clustering with high probability.

Minimax

Theorem: $P_{\Sigma}$ the likelihood based on $n$ independent observations of ${ X} \stackrel{d}{=} \mathcal{N}(0,\Sigma)$. For any \begin{equation}\label{etamin} 0\leq \eta \lt \eta^{*}:={\sqrt{\log(p(p-1)/2)}\over \sqrt{(2+e^{-1})n} +\sqrt{\log(p(p-1)/2)}}\,, \end{equation} we have $$\inf_{\widehat G}\sup_{R \in \mathcal{R}(\eta)} P_{\Sigma}(\widehat G\neq G^{\beta}(X))\geq {1\over 2e+1}\geq {1\over 7} \,,$$ where the infimum is taken over all possible estimators.

Group separation condition on $\eta$ is necessary.

Simulations

Setup

  • Generate from various $C$: block, sparse, negative
  • Compare:
    • Exact recovery of groups (theoretical tuning parameter)
    • Cross validation (data-driven tuning parameter)
    • Cord metric vs (semi)parametetric cor (regardless of tuning)

Exact Recovery

Block
Sparse
Negative


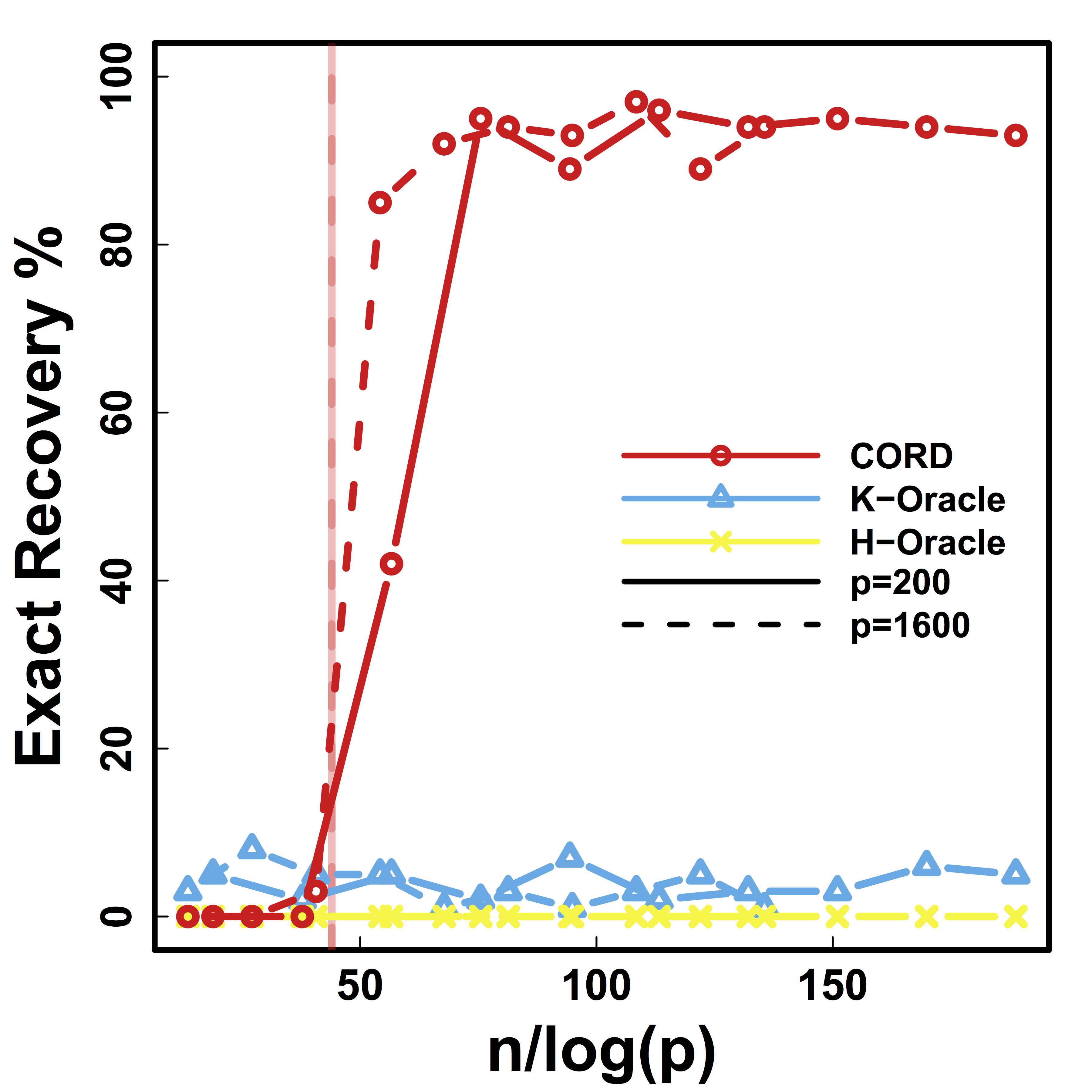
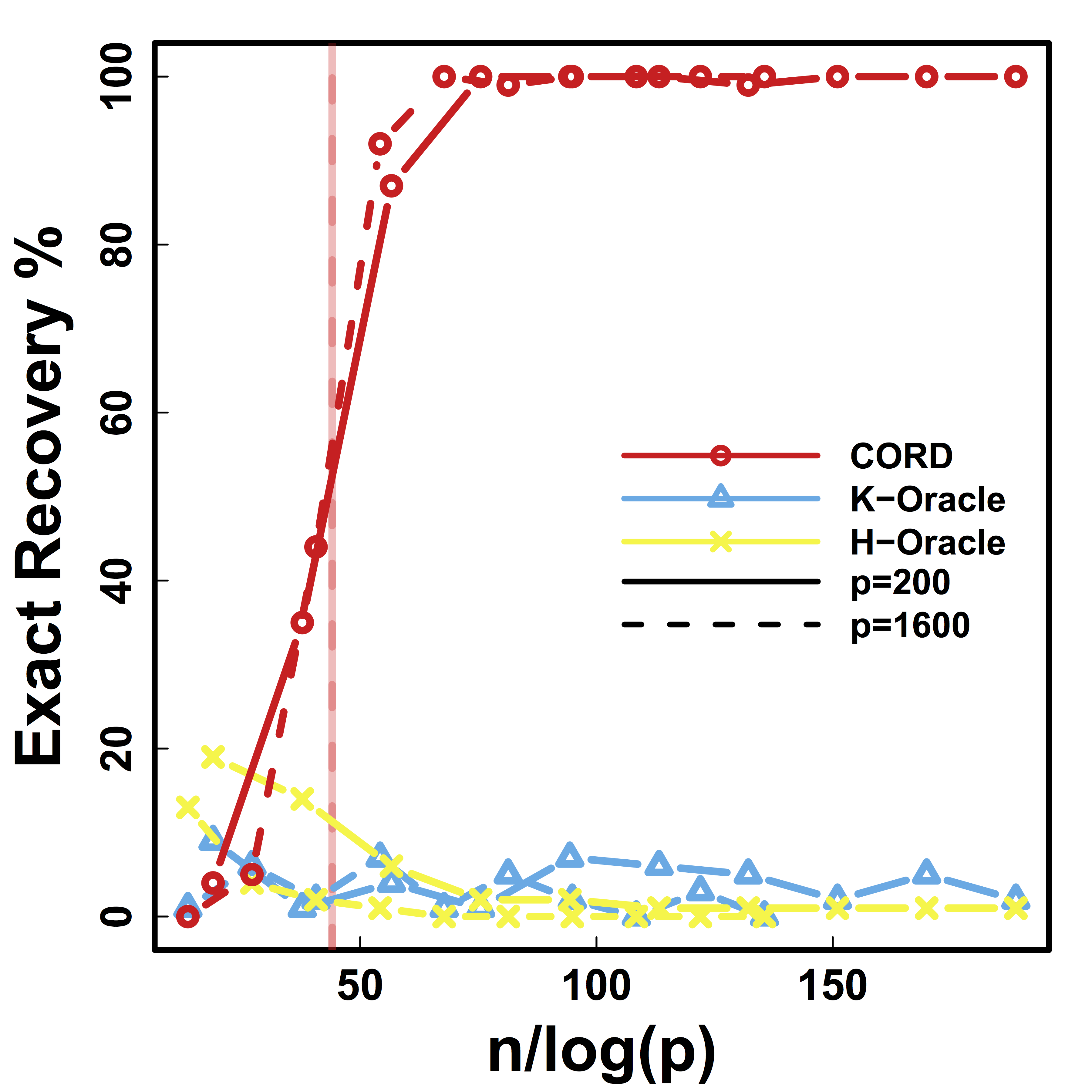
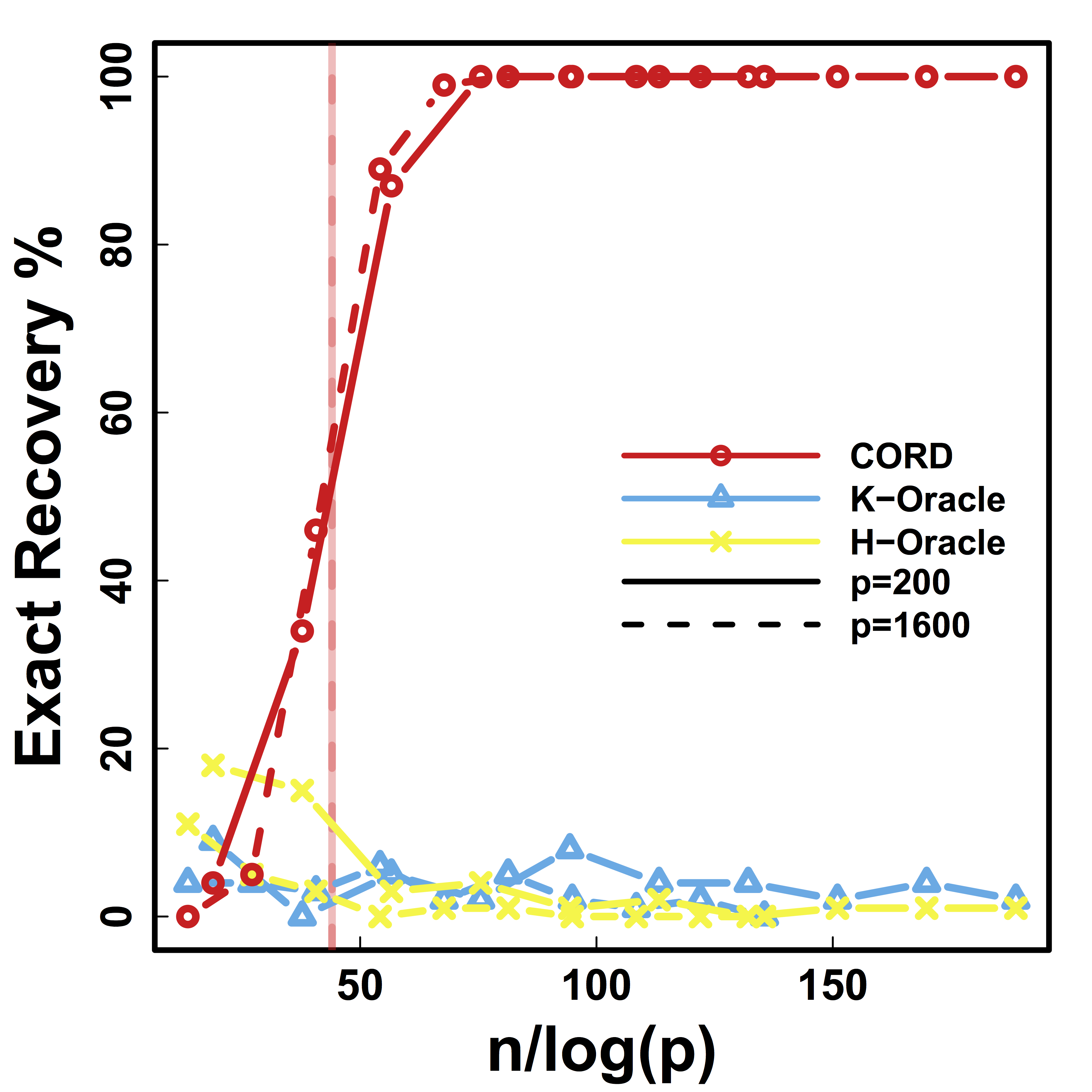
Different models for $C$="$\cov(Z)$" and $\alpha = 2 n^{-1/2} \log^{1/2} p$

Vertical lines: theoretical sample size based on our lower bound

HC and Kmeans fail even if inputting the true $K$.

Data-driven choice of $\alpha$

  • Given $G$ and $R$, we introduce a block averaging operator $\left[\varUpsilon\left(R,G\right)\right]_{ab} =$ $$\begin{cases} \left|G_{k}\right|^{-1}\left(\left|G_{k}\right|-1\right)^{-1}\sum_{i,j\in G_{k},i\ne j}R_{ij} & \mbox{if } a\ne b \mbox{ and } k=k^{\prime}\\ \left|G_{k}\right|^{-1}\left|G_{k^{\prime}}\right|^{-1}\sum_{i\in G_{k},j\in G_{k^{\prime}}}R_{ij} & \mbox{if } a\ne b \mbox{ and } k\ne k^{\prime}\\ 1 & \mbox{if }a=b. \end{cases} $$
  • We choose $\alpha$ via cross validation using minimization over a grid of $\alpha$: $$\min_\alpha \| \varUpsilon\left(\hat R,G_\alpha \right) - \hat{R}_{test}\|_F^2 $$

Cross Validation


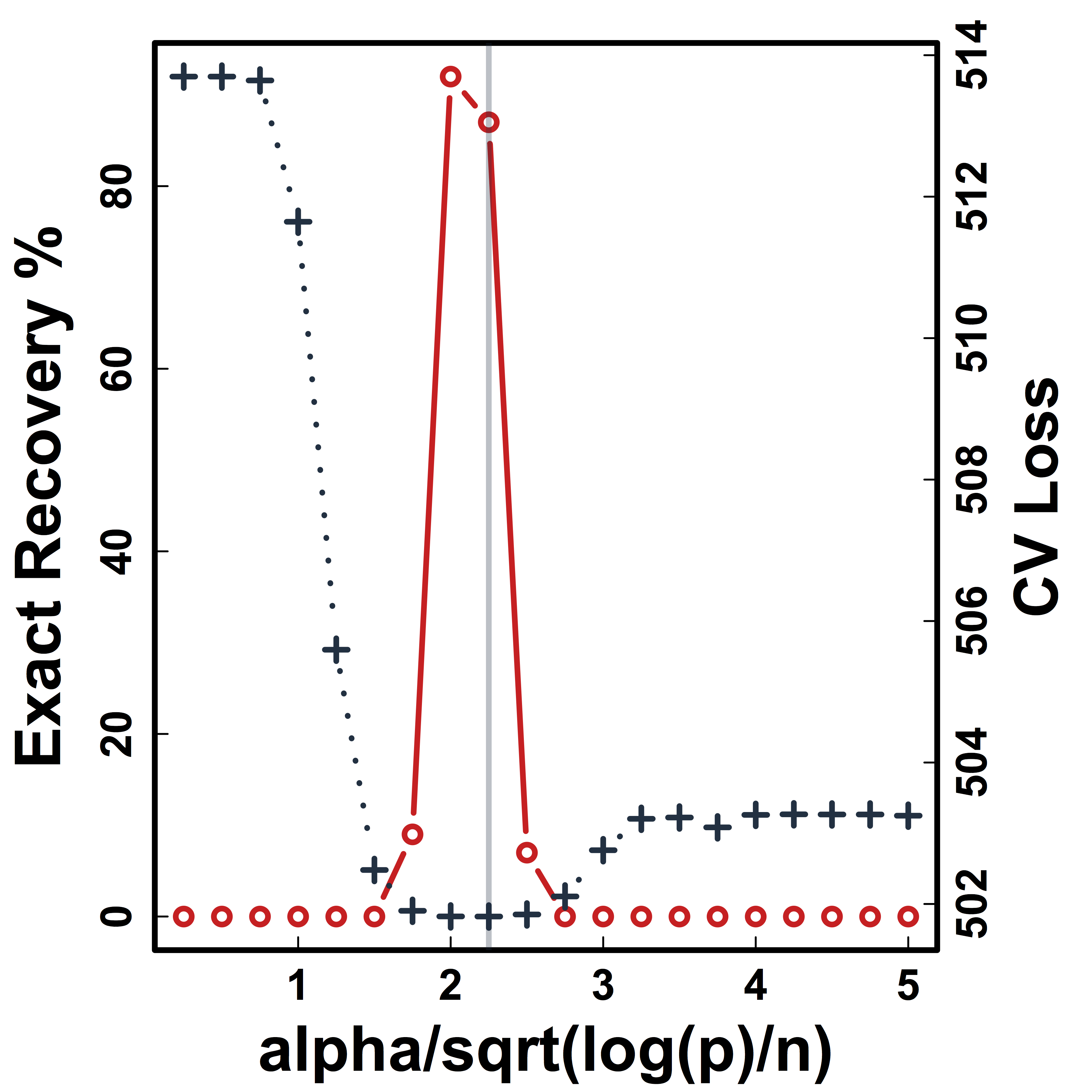
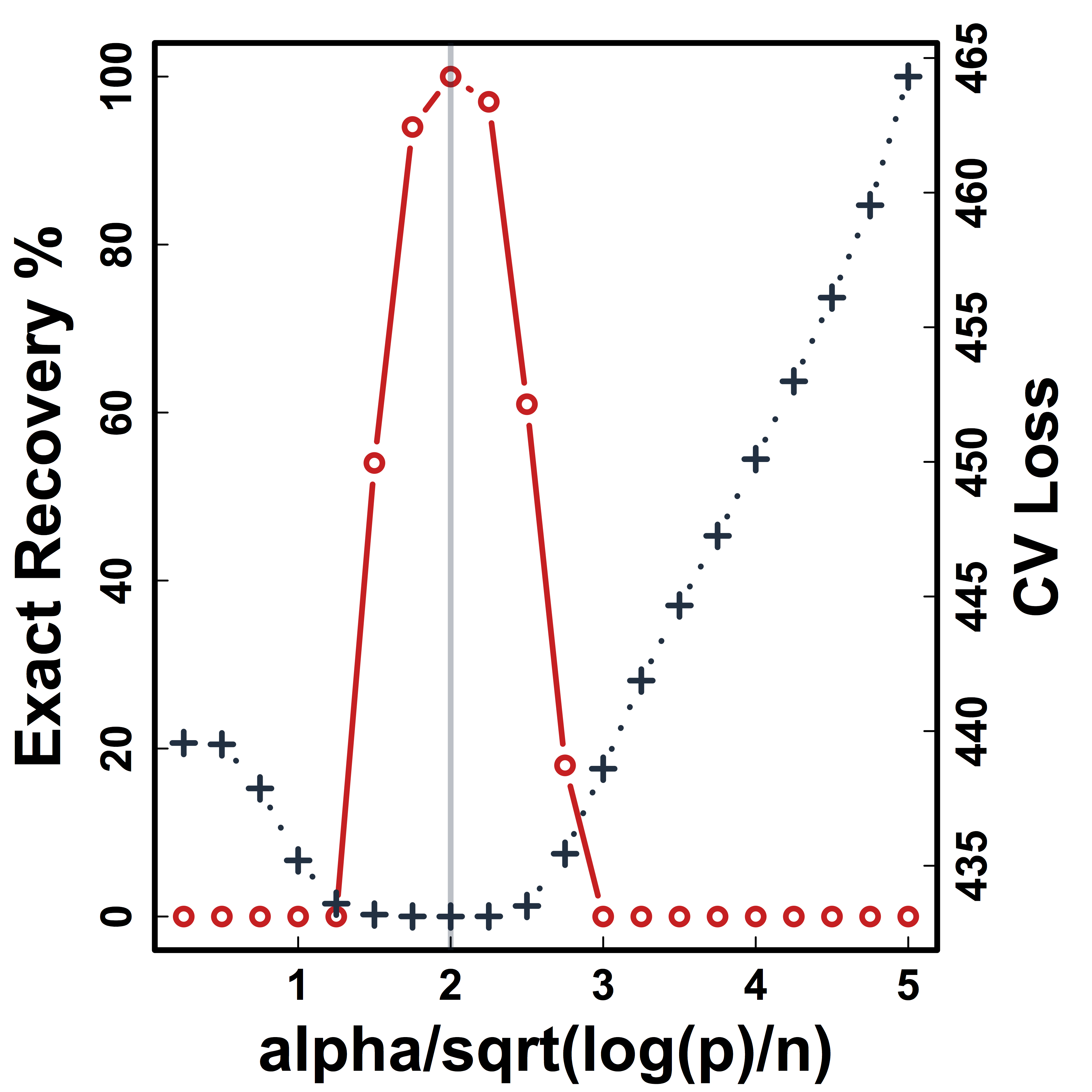
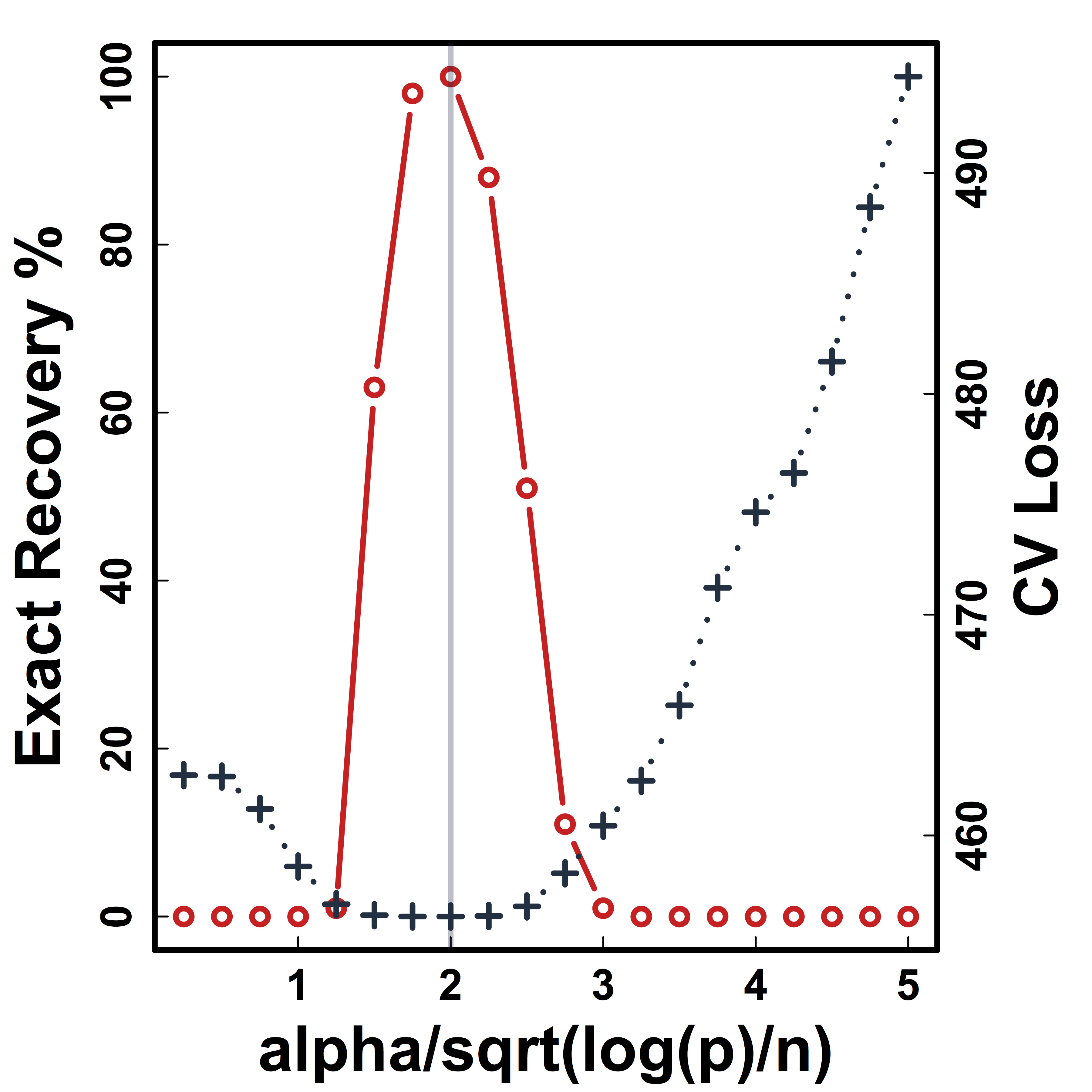
Recovery % in red and CV loss in black.

CV selects the constants to yield close to 100% recovery.

Metric Comparison: Without Threhold

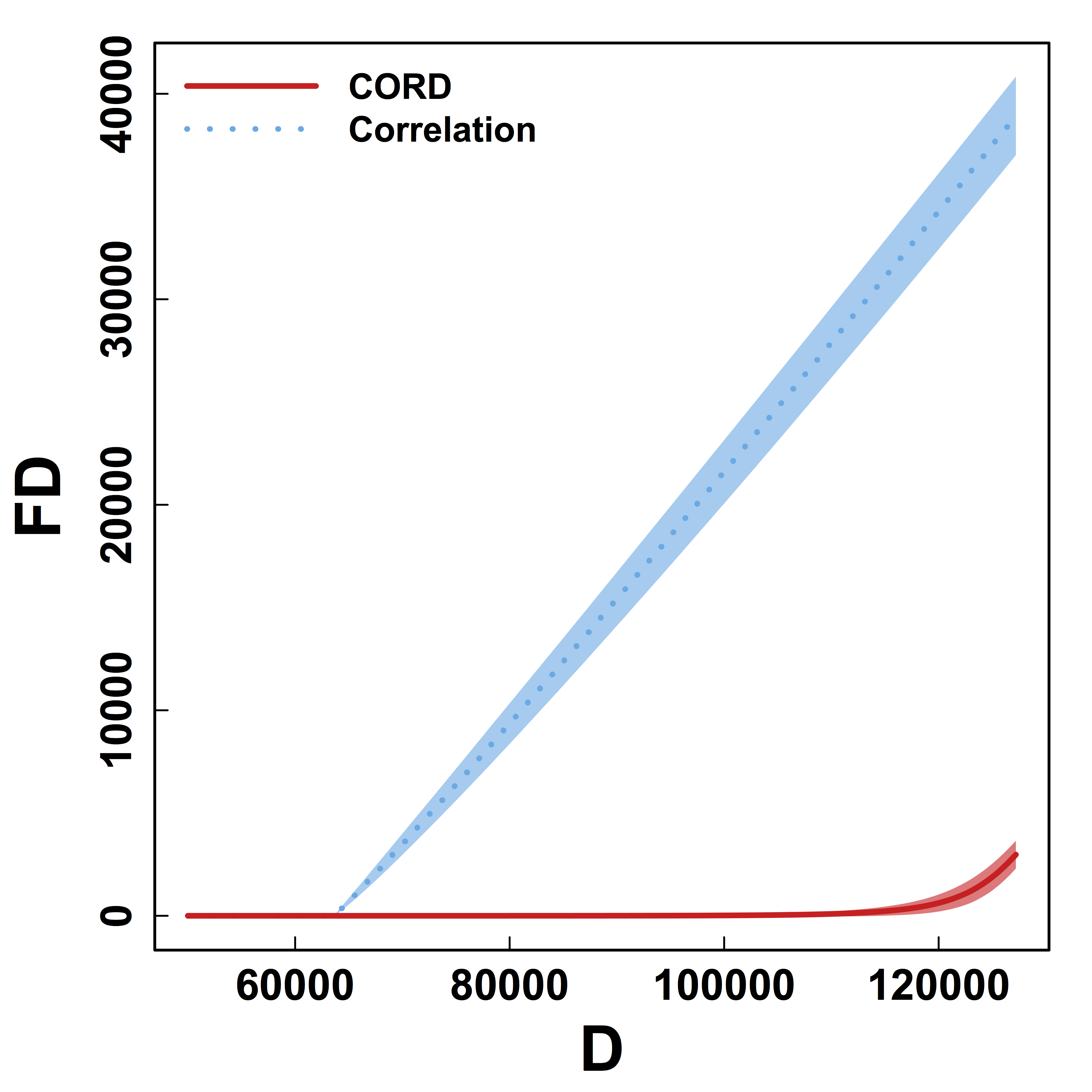
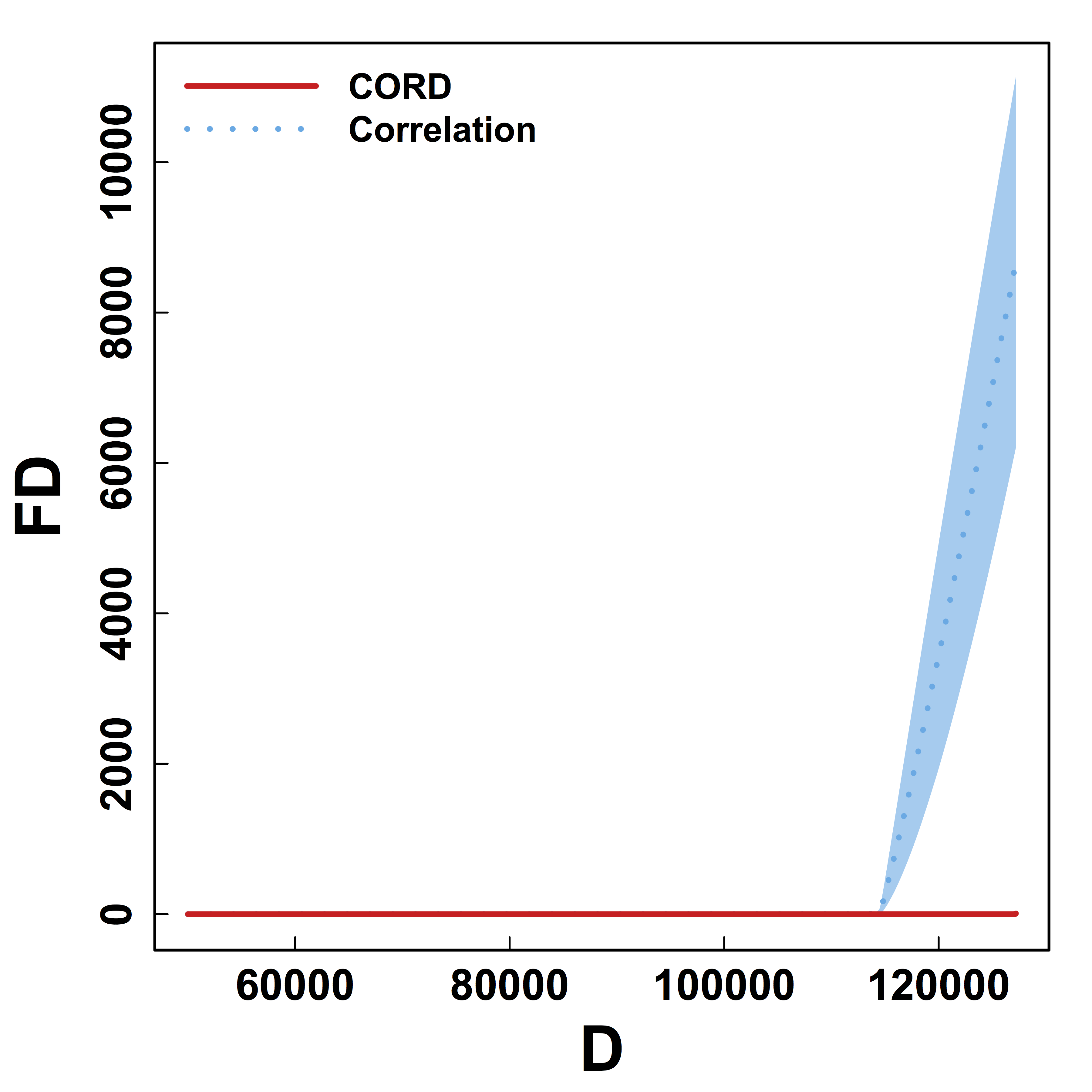
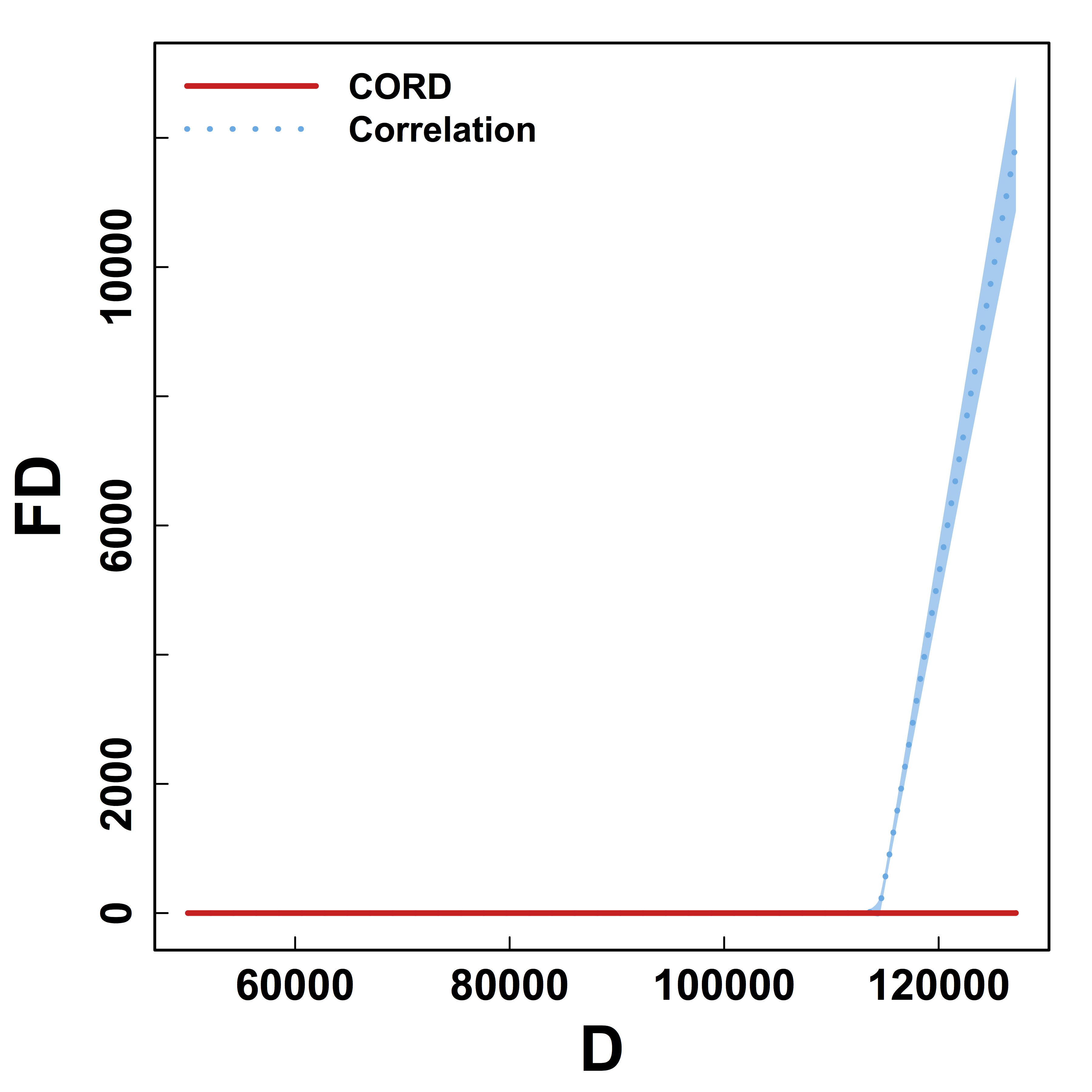
HC and Kmeans metrics yield more false discoveries (FD) as the threshold (or $K$) varies.


Better metric for clustering regardless of threshold.

Real Data

fMRI data: blood-oxygen-level dependent (BOLD) signals from each cube/voxel (~millimeters), $10^5$ ~ $10^6$ voxels in total.

fMRI Studies

Sub 1, Sess 1

Time 1

2

…

~200


⋮

Sub i, Sess j

…

⋮

Sub ~100, Sess ~4

…



This talk: one subject, two sessions (to test replicability)

Functional MRI

  • fMRI matrix: BOLD from different brain regions
    • Variable: different brain regions
    • Sample: time series (after whitening or removing temporal correlations)
    • Clusters of brain regions
  • Two data matrices from two scan sessions OpenfMRI.org
  • Use Power's 264 regions/nodes

Test Prediction/Reproducibilty

  • Find partitions using the first session data
  • Average each block cor to improve estimation
  • Compare with the cor matrix from the second scan $$ \| Avg_{\hat{G}}(\hat{\Sigma}_1) - \hat{\Sigma}_2 \|$$
  • Difference is smaller if clustering $\hat{G}$ is better

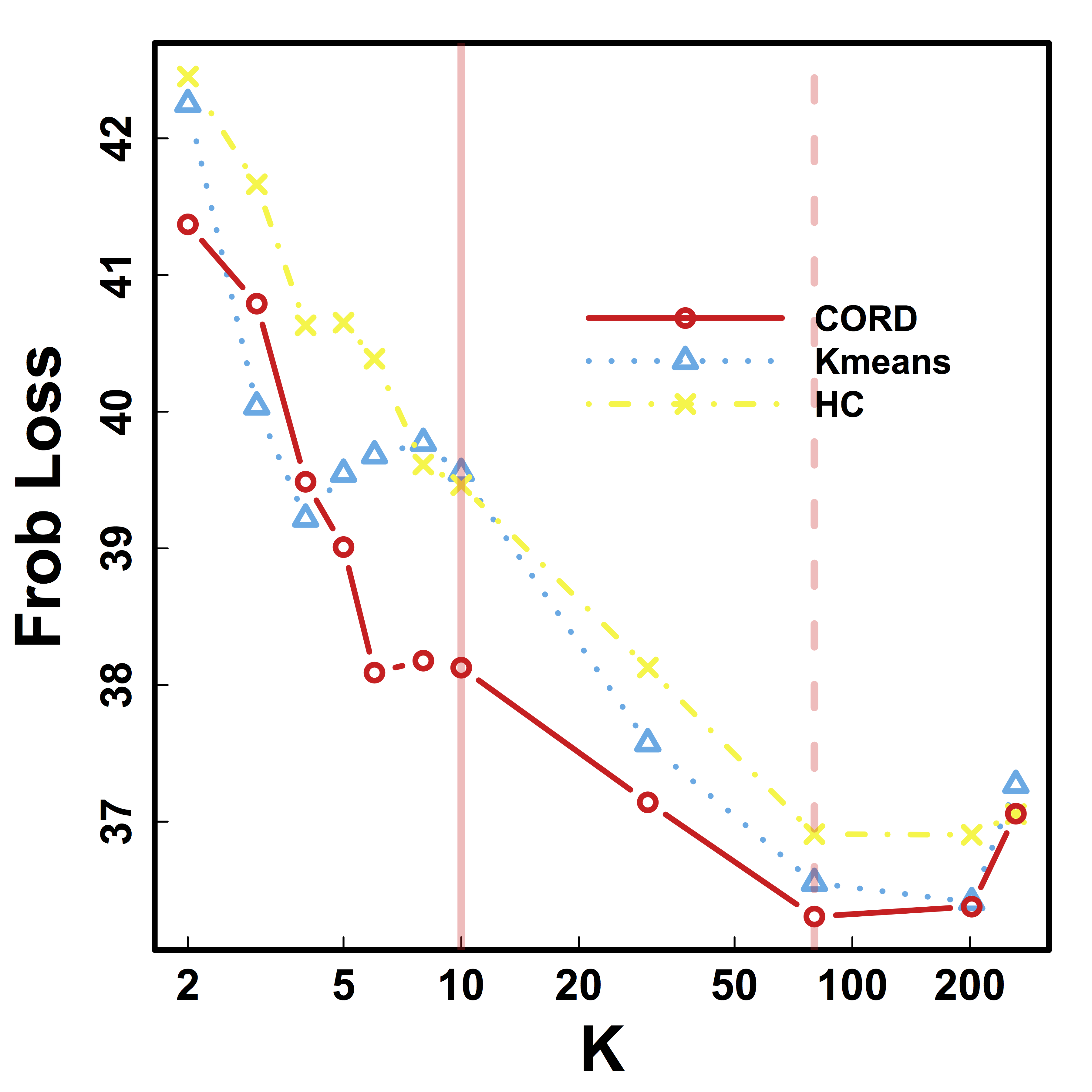
Vertical lines: fixed (solid) and data-driven (dashed) thresholds

Prediction Comparison: smaller prediction loss for almost all $K$

Discussion

  • Cov + clustering:
    • Identifiability, accuracy, optimality
  • $G$-models: $G$-latent, $G$-block, $G$-exchangeable
  • New metric, method, and theory
  • Paper: google "cord clustering"(arXiv 1508.01939)
  • R package: cord on CRAN

Thank you!


Slides at: bit.ly/SLDS16

Website: BigComplexData.com